Indice dei Contenuti
Il teorema della pizza rappresenta un assunto geometrico elementare attraverso cui la matematica ha dimostrato l’equivalenza di due aree che si ottengono dividendo un cerchio. Questo nome particolare deriva dal fatto che come metafora viene riportata proprio la pizza e il suo rispettivo taglio.
Se quindi fino ad ora non avevate mai pensato che la geometria si potesse applicare alla pizza, oggi dovrete letteralmente cambiare idea. Con molta probabilità, questa stravagante idea sarà nata durante una cena, forse proprio mentre si mangiava una pizza. Sta di fatto che i due scienziati, Mabry e Deiermann, si sono serviti della cucina per spiegare la loro idea.
Il caso
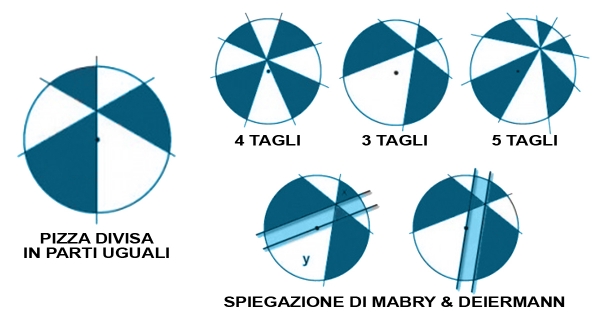
Immaginiamo che Tizio e Caio vogliano dividersi la pizza in maniera “artistica”: ovvero diversamente dalla classica linea a metà. Qualora la pizza fosse tagliata usando tre linee di cui almeno uno passa per il centro, i due amici sicuramente mangeranno la stessa quantità di pizza.
Cosa accade invece qualora i tagli della pizza non riuscissero a passare per il centro? Quando le fette sono pari, come ad esempio 4, sicuramente i due amici mangeranno in parti uguali la pizza. La teoria si basa sull’assunto per il quale, u. certo signor Upton nel 1968 affermò che “la somma delle aree dei settori dispari è uguale alla somma delle aree dei settori di numero pari”.
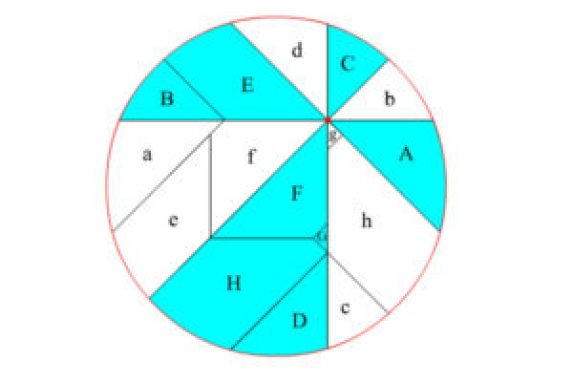
E su questo non ci piove. Ma se le parti sono dispari? La cosa ovviamente si complica. In tal caso, avverrà da un lato che mangerà di più chi ha la fetta con il centro della pizza per alcuni numeri. Viceversa, per altri numeri, mangerà di più chi ha la fetta che non ne contiene il centro.
A ben vedere nell’immagine vengono mostrati i vari casi di suddivisione, che i nostri due scienziati hanno preso in esame per raggiungere la soluzione. Diventava solo un passo accessorio quello di discutere circa la distribuzione del condimento.
La storia di Upton
Come abbiamo anticipato, a smuovere questo gioco di logica e matematica da cui nasce il teorema è stato L.J. Upton nel maggio 1968. Quest’ultimo pubblicò il suo quesito su Mathematical Magazine, e si limitava a prendere in considerazione solo lotti di pizza pari. Di seguito, il testo originale:
(EN)«Four lines in a plane are concurrent at O. The angles between the lines are each 45°. A circle is superimposed on this configuration so that O lies within the circle. (a) Show that the alternate sectors cover one-half of the circle. (b) Show this result without use of the calculus.»
(IT)«Quattro rette su un piano passano tutte per lo stesso punto O. Gli angoli fra le rette sono tutti di 45°. Una circonferenza è sovrapposta a questa configurazione in maniera che O cada all’interno del cerchio. (a) Dimostrare che i settori alterni coprono metà dell’area del cerchio. (b) Dimostrare il risultato senza fare uso del calcolo infinitesimale.
La risposta di Goldberg
Sulla medesima rivista trova pubblicazione la soluzione proposta da Michael Goldberg (Washington, D.C.). Quest’ultima richiamava l’utilizzo delle espressioni algebriche che aiutano a suddividere le aree dei settori circolari. Non solo in questo modo fu data una spiegazione al problema (ovvero mostrare che la suddivisione in otto settori è equa), Goldberg mette anche in risalto che la sua risposta va bene in qualunque caso si voglia dividere la pizza (o meglio un cerchio) in 4n + 4 settori equiangolari. Solo con questa espressione si divider equamente in n insiemi equiestesi di settori.
L’elaborazione di Carter e Wagon
Una seconda dimostrazione molto più è stata elaborata da Larry Carter e Stan Wagon, per i quali, per ogni divisione ricavata dalle ipotesi precedenti c’è una partizione dei settori. Da quest’ultima emerge che ogni blocco incluso in un settore pari sia congruente ad un corrispondente blocco contenuto in un settore dispari.